Constrained motion planning problems are problems where a set of constraints are placed on the motion of a robot. These constraints could require that parts of the robot occupy certain subsets of the workspace (e.g., for Fetch robot grasping and manipulating a binder) or that they remain in contact with each other (e.g., closed chains).
Motion planning with constraints has many applications, including the parallel robots, closed molecular chains, animation, reconfigurable robots, and grasping for single and multiple robots.
Constrained problems are particularly challenging because they require that the robot satisfy a problem’s constraints in addition to any validity conditions associated with the problem. Traditional motion planning methods will fail because probability of generating a sample which satisfies these constraints is zero. We reparameterize the problem through reachable volumes such that generating constraint-satisfying samples is trivial. Our method applies to robots with combinations of spherical, planar, revolute, and prismatic joints.
Collaborators: Troy McMahon, Nancy Amato
Supported by: NSF
Reachable Distances for Planar Linkages
Instead of randomly sampling in the joint angle space to find closed configurations, we overcome this challenge by precomputing the subspace where closed constraints are satisfied and then directly sampling in this subspace. We represent the chain as a hierarchy of sub-chains by recursively breaking down the problem into smaller subproblems. Each sub-chain in the hierarchy may be partitioned into other, smaller sub-chains forming a closed loop. For any sub-chain, we can compute the attainable distance (reachable distance or length) between its two endpoints recursively. Instead of randomly sampling in the joint angle space, we recursively sample in the reachable distance space. This provides distinct advantages over traditional approaches:
- Joint angles are quickly and easily calculated using basic trigonometry relationships instead of using more expensive inverse kinematics solvers
- Configurations are guaranteed to satisfy closure constraints
Our method can be used to significantly improve the performance of sampling-based planners for closed-chain systems such as Probabilistic Roadmap Methods(PRM) and Rapidly-Exploring Randomized Trees. We provide the necessary motion planning primitives (namely sampling and local planning) to implement most sampling-based motion planners. Our experimental results show that our method is fast and efficient in practice making sampling configurations with closure constraints comparable to sampling open chain configurations that ignore closure constraints entirely. It is easy to implement and general. It is also extends to more distance-related constraints besides the ones demonstrated here.
- A grasping experiment where 2 articulated arms collaborate to grasp an object and transport it from one end of the environment to the other. Each arm is composed of 3 links with variable lengths.
- A fixed-base 20 link closed chain in an environment without obstacles. The links have variable lengths. The chain (red) travels from the start (green) to the goal (orange).
Reachable Volumes for General Linkages
We introduce a new concept, called reachable volumes, that are a geometric representation of the regions the joints and end effectors of a robot can reach, and use it to define a new planning space called RV-space where all points automatically satisfy robot-specific constraints. Constraints include joint closure constraints and constraints on the position of individual joints (including the end effector).
Samples and paths generated in RV-space naturally conform to constraints, making planning for constrained systems no more difficult than planning for unconstrained systems. Consequently, constrained motion planning problems that were previously difficult or unsolvable become manageable and in many cases trivial.
This method is applicable to high degree of freedom linkages, closed chains and tree-like robots with spherical, prismatic and planar articulated joints (and combinations thereof). Reachable volumes can be used to guide robot design and assist in robot operation by allowing the operator to see what portions of the robot can reach.
We develop reachable volume aware primitives for sampling-based motion planning including sampling, local planning, and computing distance. These primitives are used to realize both styles of sampling-based motion planning: PRMs and RRTs.
Reachable Volumes Illustrations
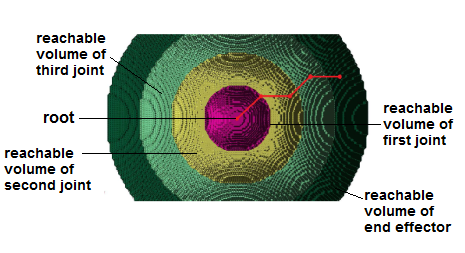
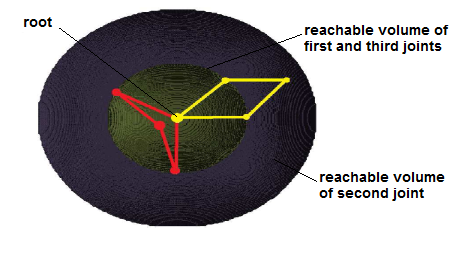
RV-space encodes the intrinsic constraints of the robot. It is independent of the environment. Just as with traditional configuration space (C-space), collision checking must be preformed separately. Below, we provide visualizations of the reachable volumes for several different linkages. In each example, the linkage is displayed in red, and the reachable volume for each joint is shaded in a different color.
- Reachable volumes of a 4 link chain with spherical joints: The first joint can reach anywhere on the pink shell. The second joint can reach anywhere within the yellow sphere (including the region inside the pink shell). The third joint can reach anywhere within the mint sphere. The end effector can reach anywhere inside of the green sphere.
- Reachable volumes of a closed chain with 4 links of equal length: The first and third joints can reach anywhere on the green shell. The second joint can reach anywhere within the blue sphere (including the region inside of the green shell).
- Reachable volumes of a 4 link fixed-base grasper with spherical joints with constraints on the end effector: The reachable volume of the base (teal) given constraints on the end effectors to grasp a cubic object (blue and green).
Reachable Volume Sampling
We also develop a family of samplers that use reachable volumes to generate samples for a wide variety of motion planning problems including end effector constraints, closure constraints, and constraints on joint positions with as many as 256 degrees of freedom.
Reachable Volume sampling iteratively places joints in their available reachable volume until all joints have been placed. Before any joints are placed, all joints have their original/full reachable volume. Once a joint is placed, this implies an additional constraint to the system which restricts the available reachable volume of other joints (e.g., neighboring joints). To place a joint, we first compute its updated reachable volume based on any previously placed joints. We then randomly select a joint placement from this reduced set. At each placement, the unplaced reachable volumes become restricted.
Reachable Volume Local Planning
We also present a reachable volume-based local planner. Just like the sampler, it guarantees that the local plan will satisfy constraints. The local planner works by iteratively stepping joints in RV-space and updating affected available reachable volumes:
- Initial joint placements.
- Step first joint.
- Update reachable volumes of neighboring joints.
- Step neighboring joints.
- Final joint placements.
Reachable Volume Distance Metric
The reachable volume distance metric captures the distance traversed during reachable volume stepping (and local planning). It is a weighted sum of the Euclidean distance between the robot base placements in workspace and the Euclidean distance between the joints placements in RV-space.

The reachable volume distance between two samples (black and gray) is the sum f the distances between their joint placements in RV-space.
Directed Reachable Volumes

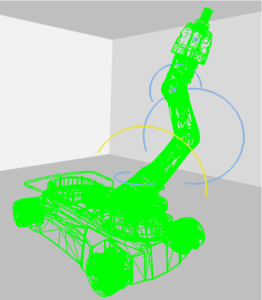
Examples of robots that employ revolute joints: a SCARA fixed base manipulator and a mobile KUKA Youbot.
Reachable volumes have been highly successful in solving constrained problems and problems with many degrees of freedom, but they cannot handle rotational joints. We develop directed reachable volumes (DRVs) which reparameterizes traditional configuration space into a new planning space called DRV-space. DRV-space makes planning the motion of a Fetch robot (composed of several revolute joints) to extract binders and place them in a bin feasible.
Rotational joints often appear in industrial robots because they weigh less and are more cost effective than spherical joints. Motion planning for manipulators with rotational joints is challenging because the actuation range for each link is constrained by the placement and orientation of other links.
DRV-space encodes the oriented volume of workspace that individual joints can access in the context of how other joints are placed. DRVs extend the concept of reachable volumes (RVs) to handle rotational joints in addition to spherical and prismatic joints. DRVs are also able to handle constraints on the orientation as well as the position of a robot’s joints and end-effectors. (RVs only handle positional constraints.)
- DRVs (blue and yellow regions) for the Kuka Youbot’s joints.
- Pick and place problem requires the Youbot to position its arm inside a cupboard for a grasping maneuver and then move to a drop-off container.
We demonstrate DRVs in the context of sampling based motion planning to solve pick-and-place problems with the KUKA Youbot. We study 2 different versions of the manipulator: the standard 5 degree of freedom arm and a 7 degree of freedom arm with 2 additional links. We also vary the pick position from the front of the cupboard, the middle of the cupboard and the back of the cupboard.