Motion planning is a difficult and widely studied problem in robotics. Current research aims not only to find feasible paths, but to ensure paths have certain properties, e.g., shortest or safest paths. This is difficult for current state-of-the-art sampling-based techniques as they typically focus on simply finding any path.
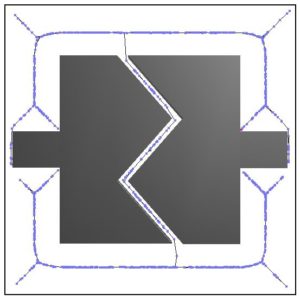
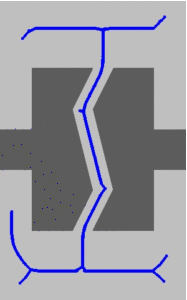
The medial axis is the set of all points equidistant between two or more obstacle boundaries. For an n-dimensional space, the medial axis is an n-1-dimensional manifold which represents the connectivity of the space. Thus, the medial axis is a useful tool for computing high clearance motions and paths.
We use the observation that any point, free or not, may be retracted to the medial axis by monitoring when the witness point (for collision) changes during the retraction. We use this function to apply medial axis retraction two two large classes of sampling based motion planning algorithms: PRMs and RRTs. We develop two sampling-based algorithms: MAPRM and MARRT and show their effectiveness in solving narrow passage problems and generating high clearance solutions.
- MAPRM
- MARRT
MAPRM
We propose a general framework for sampling the configuration space in which randomly generated configurations, free or not, are retracted onto the medial axis of the free space. This framework provides a template encompassing both exact and approximate retraction approaches.
- Uniform PRM
- MAPRM
- Uniform PRM
- MAPRM
The fundamental primitive operations are the computation of penetration depth and clearance in configuration space. As these quantities can only be computed efficiently in low-dimensional C-space, the application to high-dimensional problems employs approximate clearance and penetration depth calculations. Thus, our framework supports methods that exactly or approximately retract a given configuration onto the medial axis. Exact methods provide fast and accurate retraction in low (2 or 3) dimensional space, while approximate methods extend the method to high dimensional problems, such as many DOF articulated robots.
Theoretical and experimental results show improved performance on problems requiring traversal of narrow passages. We also study the trade-offs between accuracy and efficiency for different levels of approximation, and investigate how the level of approximation affects the quality of the resulting roadmap.
MARRT
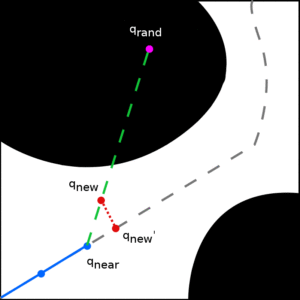
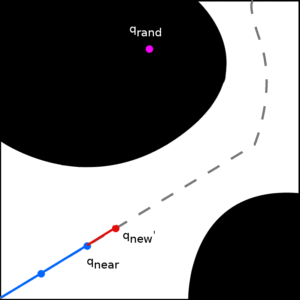
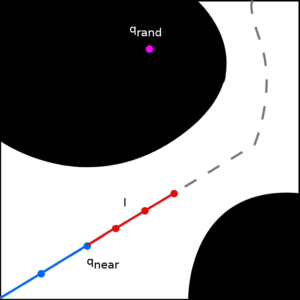
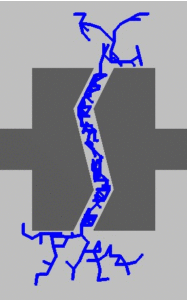
Here we apply our medial axis planning framework to Rapidly Exploring Random Trees (RRTs). RRTs search the planning space by biasing exploration toward unexplored regions. We introduce a novel RRT variant, Medial Axis RRT (MARRT), which biases tree exploration to the medial axis of the free space by pushing all configurations from expansion steps towards the medial axis. We prove that this biasing increases the tree’s clearance from obstacles. Improving obstacle clearance is useful where path safety is important, e.g., path planning for robots performing tasks in close proximity to the elderly. We also experimentally analyze MARRT, emphasizing its ability to effectively map difficult passages while increasing obstacle clearance, and compare it to contemporary RRT techniques.
MARRT differs from RRT in that instead of growing from the tree directly toward a random configuration, it constrains the growth near the medial axis. It does so by taking a small step towards the random configuration and then pushes the resulting intermediate configuration to the medial axis. It repeats this expansion process until it reaches the maximum expansion length or fails to make progress.
This process allows growth to be nicely constrained to the medial axis as compared to different RRT variants:
- RRT
- RRTObst
- RRT*
- OBRRT
- MARRT