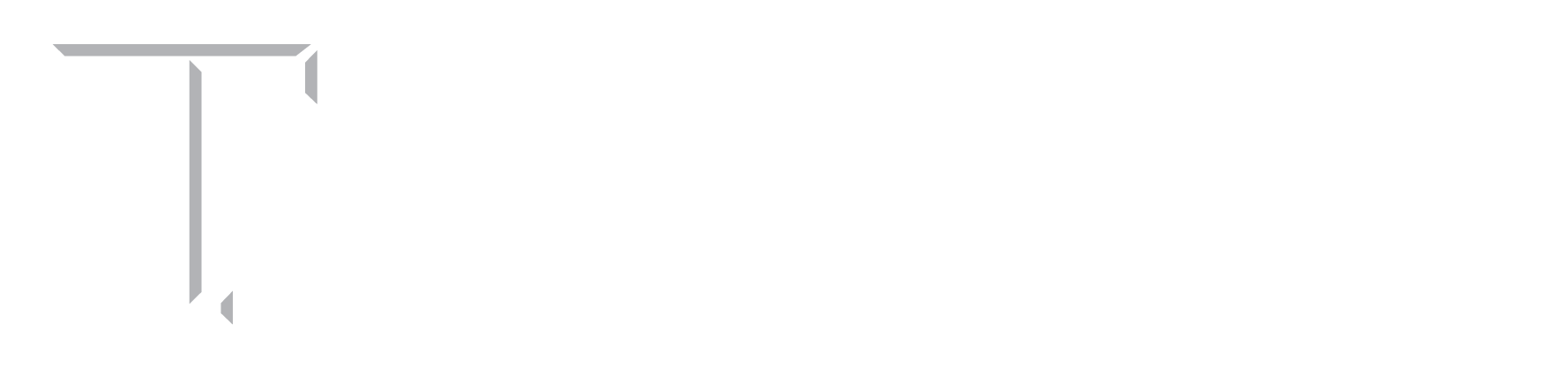Motion planning algorithms can be applied to any type of robot, from simple rigid bodies to complex articulated linkages by abstracting the particular motion planning problem into configuration space (C-space) where each point in C-space represents a particular configuration/placement of the robot. Invalid configurations (e.g., in-collision, high energy) become C-obstacles in this higher dimensional space. We can then plan the path of the (now point) robot in C-space and later transform it back to the actual robot.
Sampling based motion planning uses randomization to construct a graph or tree (roadmap) in C-space on which queries (start/goal configurations) may be solved. We explore different general purpose frameworks for sampling based motion planning to improve planner performance or customize result for different planning preferences.
Frameworks for Improved Performance
- Hierarchical Aggregation
- Incremental Map Generation
Hierarchical Aggregation
Aggregation, a key technique in manipulating geometric objects, is a form of approximation that groups objects together as a single entity. This can improve the efficiency of future processing, reduce complexity and generate levels of detail. We present a general framework to aggregate nearby objects together. Grouped objects are approximated into shapes similar to alpha shapes and reduce the space covered as compared to a convex hull approximation. As traditional alpha shapes fail to adapt to non-uniform inputs, we use a function to adaptively determine the value of alpha to approximate the shape connecting disconnected objects. Finally, we apply this framework to improve sampling based motion planning performance.
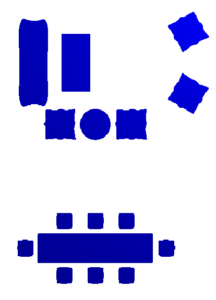
- Original boxes environment.
- Level N aggregation.
- Level N planning.
- Level N-1 aggregation.
- Level N-1 planning.
First, the environment is abstracted in form of a graph called neighborhood graph with the objects as vertices and edges represent neighborhood relation with minimum distance between the objects as the weight of the edge. We use a distance threshold, δ, to determine which objects are nearby. The edges in the neighborhood graph with weight less than δ are collapsed such that the graph corresponds to the aggregated environment.
To construct the shape of the aggregated objects, which are the vertices in the resulting neighborhood graph, we use an approach similar to alpha shape construction. We iteratively remove the triangles from the Constrained Delaunay Triangulation (CDT)/Tetrahedralization of the free space. The CDT edge and its adjacent triangle/tetrahedron to be removed must have at least one edge whose length is greater than a value determined by a function called aggregate function.
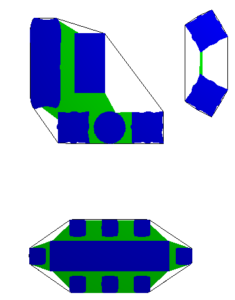
- Aggregated Model
Using the aggregation function, our aggregation produces more intuitive connection with less wasted free space as compared to convex hull.
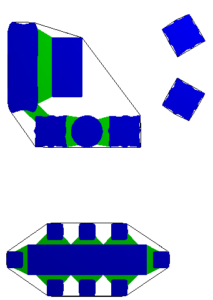
- Original office environment
- Alpha shapes aggregation (convex hull boundaries shown in black)
- Our aggregation (convex hull boundaries shown in black)
Varying the distance threshold δ, a hierarchy of aggregation can be created for any environment.
- δ = 10
- δ = 20
- δ = 30
- δ = 40
- δ = 50
- δ = 60
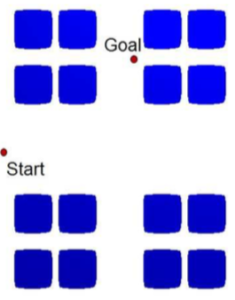
We apply the hierarchical aggregation of the obstacles to improve sampling based motion planning performance. This is achieved by iteratively sampling in the free space difference between consecutive levels in the hierarchy till the problem is solved. The idea is to plan in wider regions before the narrow or cluttered regions in the environment. We see significant performance improvements, regardless of the underlying sampler, in a variety of environments. Note that here data is normalized to the planning time without the hierarchical aggregation framework.
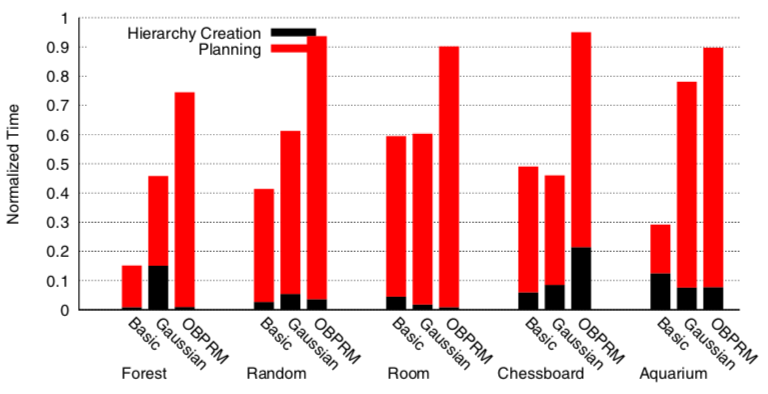
Planning time for various underlying planners for each environment. Data is normalized to the time spent by each underlying planner without the aggregation framework.
Incremental Map Generation
Probabilistic Roadmap Methods (PRMs), while highly successful in solving many high degree of freedom motion planning problems, do not provide an automated stopping mechanism to determine how large a roadmap is needed for a given problem. Ideally, planning should stop when the planner is no longer learning, when it is no longer adding useful information to the roadmap. We develop a new framework called Incremental Map Generation (IMG) to address this issue.
We break map generation into several processes, each of which generates samples and connections, and to continue adding the next increment of samples and connections to the evolving roadmap. The process continues until the planning strategy is no longer improving the roadmap as determined by a set of evaluation criteria.
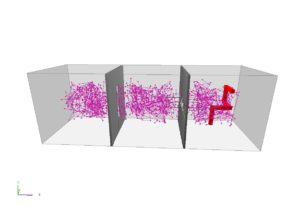
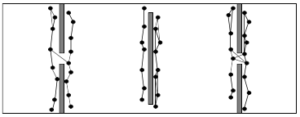
For example, consider how the roadmap below evolves over time. After 500 nodes there are 3 connected components, 2 connected components after 750 nodes, and 1 single connected component after 1000 nodes. The success rate is the percentage of queries the roadmap can solve.
- 500 nodes, solves 33.7% of queries.
- 750 nodes, solves 52.4% of queries.
- 1000 nodes, solves 98.0% of queries.
We have proposed several different evaluation criteria to control roadmap construction:
| Evaluation Criteria | |
|---|---|
| Roadmap Progress Evaluation | Monitors roadmap coverage and connectivity. Classifies new samples as they are inserted into the roadmap, and use changes in connected component diameters to approximate changes in roadmap coverage and connectivity. Stops construction when the rate of change of the maximum component diameter and the sum of component diameters over a certain period of time (k) falls below a threshold (tau). |
| Query Evaluation (Application Specific) |
Determines whether a roadmap can solve a set of user specified queries. This is useful when the user knows the set of test problems they want to solve a priori or to develop a single query application. |
| Max-flow Evaluation (Application Specific) |
For applications that require many paths between the start and goal. Monitors the maximum flow of the graph between the start and the goal set. |
Frameworks for Customizing Results
- Biasing Samplers to Improve Motion Planning Performance
- C-PRM: An Efficient, Adaptable, and Customizable PRM
Biasing Samplers to Improve Motion Planning Performance
With the success of randomized sampling-based motion planners such as Probabilistic Roadmap Methods, much work has been done to design new sampling techniques and distributions. To date, there is no sampling technique that out-performs all other techniques for all motion planning problems. Instead, each proposed technique has different strengths and weaknesses. However, little work has been done to combine these techniques to create new distributions.
In this work, we bias one sampling distribution with another such that the resulting distribution out-performs either of its parent distributions. Consider the example below. Obstacle-based sampling is able to quickly find the narrow passages but is unable to adequately sample in the free areas. Medial axis-based sampling has trouble finding these narrow passages because the walls are “thin”. However, if we combine these distributions by first sampling near obstacles and then retracting these samples to the medial axis, we can sample both narrow passages and bridge the large gaps between them.
- Obstacle-Based Sampling
- Medial Axis-Based Sampling
- Biased Sampling: Obstacle-Based Sampling to bias Medial-Axis Based Sampling
We develop a general framework for biasing samplers that is easily extendable to new distributions and can handle an arbitrary number of parent distributions by chaining them together. Our biased sampling framework is simple and general. Any component sampler may be used as long as it has a method to output a new sample biased by an input sample (such as perturbed or filtered).

Biasing Sampling Framework
Our experimental results show that by combining distributions, we can out-perform existing planners. Consider the S-Tunnel environment below. It contains two types of areas: free space and an extended narrow passage.

S-Tunnel
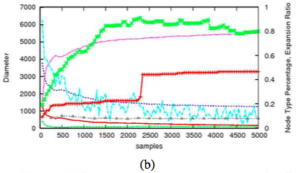
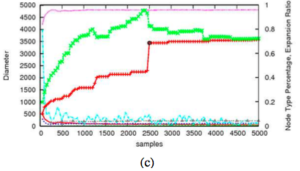
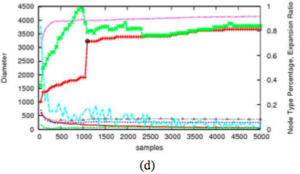
We compare for different samplers on a single random seed: uniform sampling, obstacle-based sampling, medial axis based-sampling, and biased sampling with obstacle-based samples seeding the medial axis-based sampler. All of the samplers quickly map the two free portions of the environment (as indicated by the rapid increase in the largest connected component’s diameter), but biased sampling is able to connect them via the narrow passage much faster than the others (and in some cases the others fail to do so in the time allotted).
- Uniform Sampling
- Obstacle-Based Sampling
- Medial Axis-Based Sampling
- Biased Sampling
![]()
Our results also indicate that not one single distribution combination performs the best in all problems, and we identify which perform better for the specific application domains studied.
C-PRM: An Efficient, Adaptable, and Customizable PRM
We propose a new approach for building and querying probabilistic roadmaps (PRMs). In the roadmap construction stage, we build coarse roadmaps by performing only an approximate validation of the roadmap nodes and/or edges. In the query stage, the roadmap is validated and refined only in the area of interest for the query, and moreover, is customized in accordance with any specified query preferences. This approach, which postpones some of the validation checks (e.g., collision checks) to the query phase, yields more efficient solutions to many problems.
This framework includes all previous PRM variants as special cases. In particular,
- it encompasses variable levels of validation (from none to complete) of nodes and edges during roadmap construction,
- it provides for various edge evaluation schedules when validating paths extracted from the roadmap, and
- it enables path customization to satisfy variable, adaptive query requirements.
An important benefit of our approach is that it gives one the ability to customize the same roadmap in accordance with multiple, variable, query preferences. For example, our approach enables one to find a path which maintains a particular clearance, or makes at most some specified number of sharp turns.
| Common Path Requirements | |
| Application | Requirement |
| CAD | clearance |
| Mobile robots | clearance, smoothness |
| Manipulators | singularity, clearance |
| Ligand binding | low potential energy |
Our preliminary results on problems drawn from diverse application domains show that this new approach dramatically improves performance, and shows remarkable flexibility when adapting to different query requirements.